ISO-Point Generation

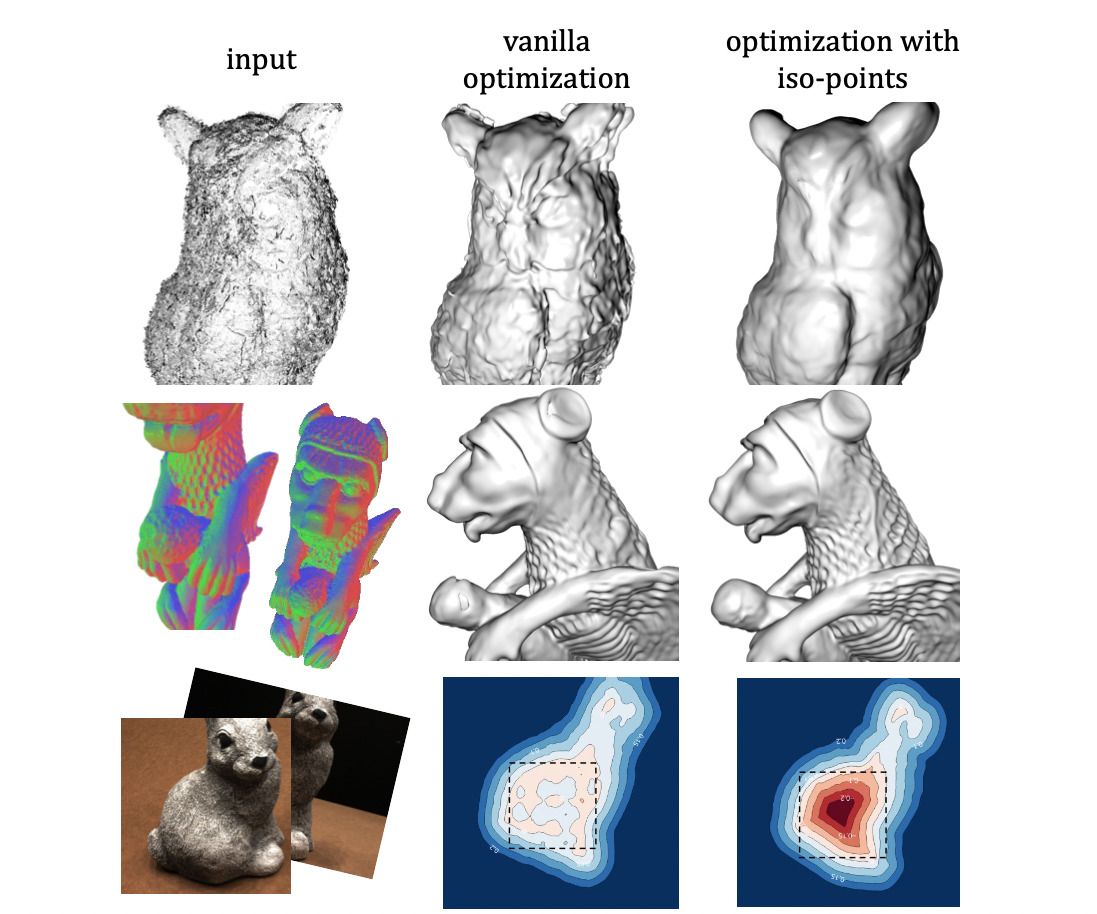
给了当前的SDF \(f_t(p;\theta_t)\),这个隐函数表示的曲面是\(\mathcal{S}_t\),ISO-points 是\(\mathcal{S}_t\) 上的一个稠密均匀分布的点集合,也就是说ISO-Points 是可以比较准确的表示这个曲面的. 也就是说, ISO-Points 是和当前的\(\mathcal{S}_t\) 相关的.

graph TD;
  A[Initial Points onto the zero level set]-- Projection -->B[A set of base iso-points];
  B--Uniform Resampling-->C[Resampled ISO-Points to avoid clusters of points and fill large holes];
  C--Upsampling-->D[Obtained Dense  and Uniformly distributed ISO-Points]

Projection

• Input:

  • Initial Points : \(\mathcal{Q}_t\)
  • Current SDF \(f_t(x;\theta_t)\)

• Output:

  • Base ISO-Points : \(\hat{q}_t\)

• Method:

  • Newton's Method

For k=1:K:

• $\mathbf{q}^{k+1}_t=\mathbf{q}^k_t-\tau\left(\frac{J_f^{\top}\left(\mathbf{q}^k_t\right)}{\left|J_f\left(\mathbf{q}^k_t\right)\right|^2} f\left(\mathbf{q}^k_t\right)\right)$
  • $\tau(\mathbf{v})=\frac{\mathbf{v}}{|\mathbf{v}|} \min \left(|\mathbf{v}|, \tau_0\right)$

At Each training iteration, \(K<=10\), when $|f(\mathbf{q}_t^k)|<\epsilon$, stop.(\(\epsilon=10^{-4}\downarrow 10^{-5}\) during training )

Uniform Resampling