Table of Contents
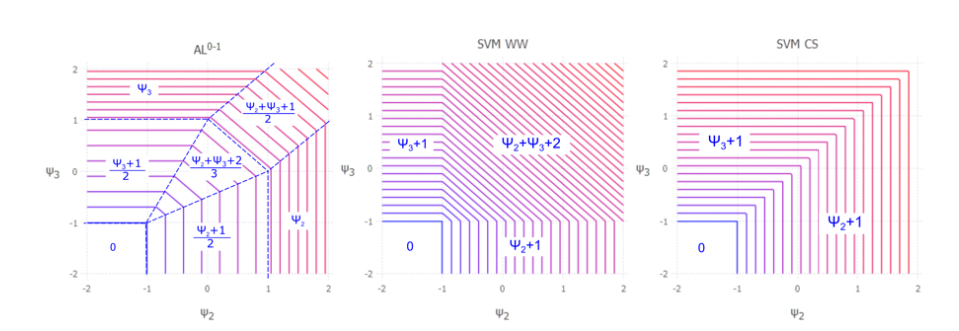
Multiclass SVM generalizations
Multiclass SVM generalizations
multiclass support vector machine (SVM) seeks class-based potentials $f_y(\mathbf{x}_i)$ for each input vector $\mathbf{x}\in \mathcal{X}$ and class $y\in \mathcal{Y}$ so that the discriminant function $\hat{y}_f(\mathbf{x}_i)=\arg\max_{y} f_y(\mathbf{x}_i)$ minimize the misclassification errors, $loss_f(\mathbf{x}_i,y_i)=I(y_i\neq \hat{y}_f(\mathbf{x}_i))$
Multiclass SVM generalizations
Empirical Risk Minimization
$$\min_f\mathbb{E}_{(\mathbf{x},y)\in P_{data}(\mathbf{x},y)}[loss_f(x,y)]$$
for Zero-one loss is NP-hard
hinge loss approximation
In the binary setting, $y_i\in \{-1,+1\}$ where the potential of one class can be set to zero($f_{-1}=0$) with no loss in generality, the hinge loss is defined as $[1-y_if_{+1}(x_i)]_+$.
Multiclass SVM generalizations
Binary SVM
is an empirical risk minimizer using the hinge loss with $L_2$ regularization,
$$\min_{f_{\theta}}\mathbb{E}_{(\mathbf{x},y)\sim P_{data}(\mathbf{x},y)}[loss_{f_{\theta}}(\mathbf{x},y)]+\frac{\lambda}{2}||\theta||_2^2$$
Adversarial prediction games
Adversarial prediction games
The empirical training data is replaced by an adversarially chosen conditional label distribution $\check{P}(\check{y}|\mathbf{x})$ that must closely approximate the training data, but otherwise seeks to maximize expected loss, while an estimator player $\hat{P}(\hat{y}|\mathbf{x})$ seeks to minimize expected loss.
Adversarial prediction games
For the zero-one loss, the prediction game is $$\min_{\hat{P}}\max_{\check{P}:\mathbb{E}_{P(\mathbf{x})\check{P}(\check{y}|\mathbf{x})}[\phi(\mathbf{x},\check{y})]=\tilde{\phi}}\mathbb{E}_{\tilde{P}(\mathbf{x})\hat{P}(\hat{y}|\mathbf{x})\check{P}(\check{y}|\mathbf{x})}[I(\hat{y}\neq \check{y})]$$
